引言

前兩天是投影的理論部分，今天來實作看看吧！順便實驗看看昨天所說的「飛機」理論～
還沒有設定IDE的讀者們，也可以趁機安裝自己想使用的IDE，對於這次的主題建議大家使用IDE來寫程式，畢竟到時候會是比較多檔案的專案，使用IDE可以避免要自己寫Makefile...

再跟大家說明一下，我使用的是Code::Blocks 16.01版本，大家也可以選擇跟我一樣的IDE，如果您是有基礎的Programmer，也可以選用自己習慣、愛用的囉！

新建專案(未來文章會簡化這些前置過程)

1. 首先新建一個專案，然後添加一個"main.c"檔：
   

2. 引入必須的標頭檔：

#include<stdio.h>  // 標準輸入輸出
#include<stdlib.h>  // 標準函式庫

3. 我們先宣告一些需要的變數：

#include<stdio.h>  // 標準輸入輸出
#include<stdlib.h>  // 標準函式庫

double esd;  // 眼睛到螢幕的距離(Eyes to Screen Distance)，也稱視野距離

int main()
{
    double x_3d = 0.0;  // 原三維座標X分量
    double y_3d = 0.0;  // 原三維座標Y分量
    double z_3d = 0.0;  // 原三維座標Z分量

    int bx = 0;  // 轉換後二維座標的X座標(螢幕上座標必須使用整數，文字的像素只有整數個)
    int by = 0;  // 轉換後二維座標的Y座標(同上)

    return 0;
}

4. 在無窮迴圈中，等待使用者輸入三維座標：

    for(;;)
    {
        printf("輸入3D座標：\n");
        scanf("%lf %lf %lf", &x_3d, &y_3d, &z_3d);  // %lf是接收double型態變數的參數
        
    }

5. 撰寫投影函數：

    int projectTo2d_x(double x, double y, double z)  // 三維座標投影到二維座標 - X分量
    {
        double ax = x;  // 已知的，實際上三維物體偏離中央的距離(ax)
        double eod = z;  // 眼睛到物體的Z軸距離(Eyes to Object Distance)
        double result = ax * (esd / eod);  // 套入公式
        return round(result);  // 四捨五入(必須為整數傳出)，數學函數，需引入"math.h"標頭檔(見下一項)
    }

    int projectTo2d_y(double x, double y, double z)  // 三維座標投影到二維座標 - Y分量
    {
        double ay = y;
        double eod = z;
        double result = ay * (esd / eod);
        return round(result);
    }

6. 由於我們使用到round四捨五入函數，我們須在開頭加上"math.h"標頭檔(也在這裡提醒使用純gcc編譯器讀者們，使用math.h的話需在編譯命令後加上"-lm"參數，才能正常使用"math.h"標頭檔)：

    #include<math.h>

7. esd取決於觀察者與觀測平面距離，這裡我們先設為10：

    esd = 10.0;  // 視野距離設為10

8. 於使用者輸入三維座標值後，使用函數進行運算，並印出來：

    for(;;)
    {
        printf("輸入3D座標：\n");
        scanf("%lf %lf %lf", &x_3d, &y_3d, &z_3d);

//新增部分
        bx = projectTo2d_x(x_3d, y_3d, z_3d);  // 轉換
        by = projectTo2d_y(x_3d, y_3d, z_3d);

        printf("原3D座標：(%f, %f, %f)\n", x_3d, y_3d, z_3d);
        printf("轉換後2D座標：(%d, %d)\n", bx, by);
//---
    }

9. 完整程式：

#include<stdio.h>
#include<stdlib.h>
#include<math.h>

double esd = 0.0;

int projectTo2d_x(double x, double y, double z)
{
    double ax = x;
    double eod = z;
    double result = ax * (esd / eod);
    return round(result);
}

int projectTo2d_y(double x, double y, double z)
{
    double ay = y;
    double eod = z;
    double result = ay * (esd / eod);
    return round(result);
}

int main(int argc, char *argv[])
{
    double x_3d = 0.0;
    double y_3d = 0.0;
    double z_3d = 0.0;

    int bx = 0;
    int by = 0;

    esd = 10.0;

    for(;;)
    {
        printf("輸入3D座標：\n");
        scanf("%lf %lf %lf", &x_3d, &y_3d, &z_3d);

        bx = projectTo2d_x(x_3d, y_3d, z_3d);
        by = projectTo2d_y(x_3d, y_3d, z_3d);

        printf("原3D座標：(%f, %f, %f)\n", x_3d, y_3d, z_3d);
        printf("轉換後2D座標：(%d, %d)\n", bx, by);
    }

    return 0;
}

完成後可以按下編譯、執行，看看轉換結果如何吧！

實驗

我們來實際測試看看兩種情況吧！

1. X, Y座標固定，Z座標逐漸變大：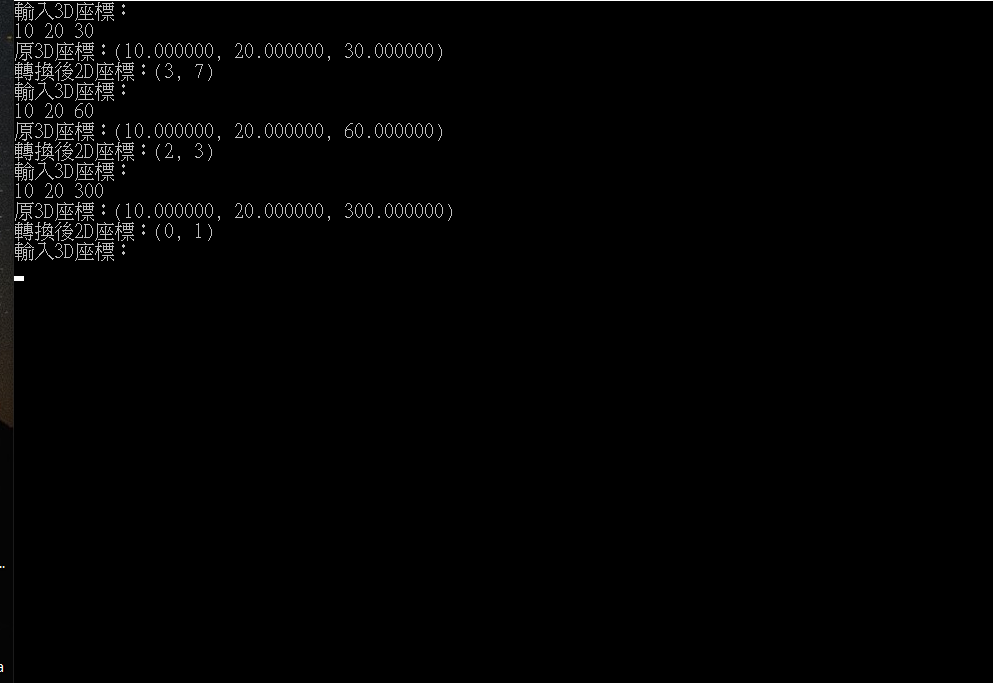
   
   若以(0, 0)為原點，我們可以觀察到雖然三者都在第一象限，但Z座標愈大，X,Y變化愈小，愈靠近原點。

2. Z座標固定，將Y座標逐漸變大，觀察投影後Y座標變化：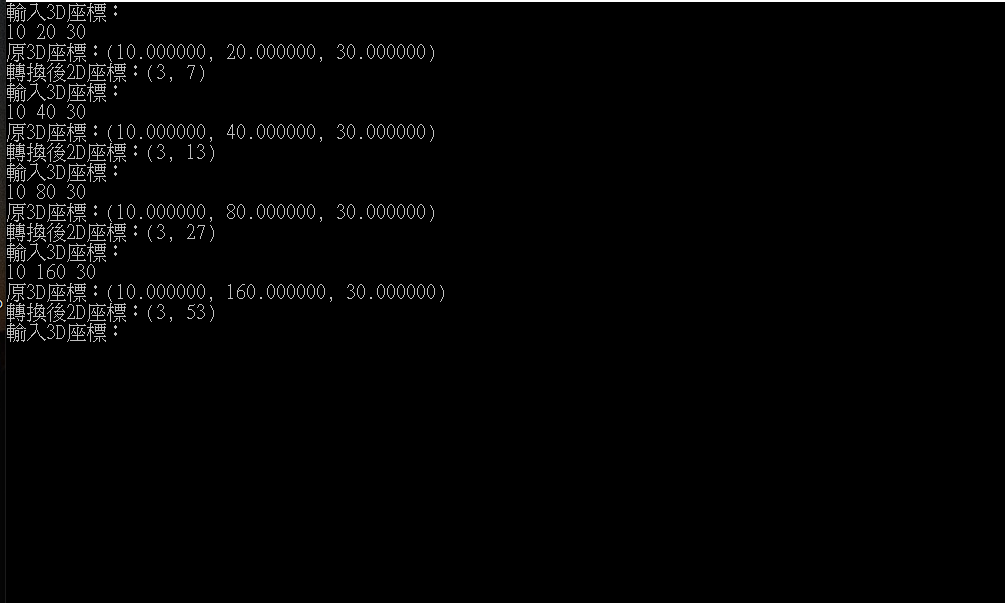
   
   從結果可以觀察出，在視野距離10、Z座標30的情況下，三維座標Y分量每移動20，大約在二維Y分量會移動6。

結語

今天的程式與實驗可以看出三維座標與轉換後二維座標的關係，之後就是利用此原理來打造出3D的引擎～